Making Forecasts in R Then Uploading to Sql Server

By:   |   Updated: 2021-03-xi   |   Comments (1)   |   Related: More > R Language

Problem

Time series forecasting has been widely employed in organizational activities. With forecasting techniques, a business concern can brand predictions and provide background information for determination-making (Moore et al., 2018). Management may inquire IT professionals to study time serial and produce forecasts. Developing time series analysis and forecasting skills helps IT professionals tackle these kinds of requests at work.

Solution

A time series, by definition, is a collection of data obtained by observing a response variable (usually denoted by y) over fourth dimension (William & Sincich 2012). Many forecasting techniques are available to predict futurity values of a time series. The best forecasting technique is not always the most complicated one. In certain situations, unproblematic methods may work better than the other more complicated methods. In this article, we explore four simple time series forecasting methods:

• The Mean Method
• The Naïve Method
• The Seasonal Naïve method
• The Unproblematic Moving Average Method

We start with ii simple forecasting methods: the mean and naïve methods. People may have already applied these two methods in daily life, fifty-fifty though their mathematical background did non include a report of fourth dimension series and forecasting.

Permit us await at a real-world state of affairs where we can utilize these 2 time serial models. Edgewood Solutions started MSSQLTips.com in 2006. From and then on, expert authors bring together the MSSQLTips.com team every year (MSSQLTips, 2021). The Tabular array one dataset presents the numbers of newly joined team members recorded every year. In this article, nosotros always presume time series data is exactly evenly spaced. The CTO at Edgewood Solutions, Jeremy Kadlec, wants to forecast the number of new members in 2021.

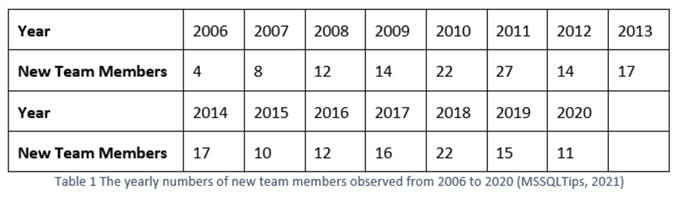
Applying no noesis of fourth dimension series analysis, we tin can use the mean (or boilerplate) of these numbers to predict the yearly number of new MSSQLTips.com team members. Nosotros use all prior observations equally to forecast the hereafter values of the fourth dimension series when adopting this algorithm. We get the mean value through this calculation:

We and so can predict that the MSSQLTips.com team welcomes 15 new members in the year 2021. The way to make this prediction is called the hateful (or boilerplate) method, which uses the mean (or average) of the historical data to predict all future values. The mean method is suitable for data that fluctuates around a abiding mean. Mathematically, nosotros tin can write this forecasting method in this form, where denotes the point forecast at the time point t:

Another simple forecasting method is the naive method. Convenience store owners may like to apply this method. For example, if the ice foam sales were $205 yesterday, they forecast the sales will be $205 today. They employ yesterday'southward sales to predict today's sales. Similarly, they can use today's sales to predict tomorrow's sales. The naive method uses simply the virtually recent observation equally hereafter values of the time series. We can utilise the following mathematical expression to represent the method:

where denotes a point forecast, denotes an observed value, and the subscripts t and (t-1) denote two adjacent time points.

We now apply this method to forecast the number of new members in 2021. Since there were eleven new members in 2020, nosotros predict that 11 experts join the squad in 2021. Every bit the proper name implies, the naive method is simple. The naïve method does not filter out any random dissonance, although it can reflect the most recent changes.

The mean method makes utilise of every piece of historical information equally to produce forecasts. On the other side, the naïve method takes only the most contempo observation. The unproblematic moving average method, something between these 2 extremes, uses several the well-nigh recent observations to generate a forecast (Stevenson, 2012). For example, given the numbers of the newly joined members in the years 2017, 2018, and 2019, nosotros so compute the 3-period moving boilerplate forecast for the twelvemonth 2020:

At the terminate of 2020, the bodily value, which is 11, becomes bachelor. So, we tin compute the moving average forecast for the yr 2021:

The calculation averages only recent observations and and so moves along to the next time period; therefore, we call these computed averages one-sided moving averages, not weighted averages. This method can handle step changes or gradual changes in the level of the series. However, it works best for a time series that fluctuates effectually an average (Stevenson, 2012). Another main way of using the moving average method is to average the time serial values over adjacent periods and obtain ii-sided moving averages. We concentrate on the one-sided moving averages in this article.

We have used three forecasting methods to predict the number of new team members in 2021. We got iii unlike forecasted values: 15, xi, and 16. When the actual number becomes available at the end of 2021, none is probable correct, leading to skepticism well-nigh forecasting. In reality, people frequently criticize a forecast for existence incorrect. The misunderstanding of forecasting is one of the most key causes of this skepticism (Goodwin, 2018). With an agreement of some forecasting techniques, nosotros can practice forecasting magic and interpret forecasts correctly.

To further explain these forecasting methods, the writer arranges the rest of the article to try to help data scientists: Department 1 explores the characteristics of a fourth dimension series and performs time serial analysis. The section likewise uses some R commands to visualize fourth dimension serial and decompose a fourth dimension series into three components for deep learning. Department two covers some mutual features of diverse forecasting techniques, uses four forecasting methods as predictors, and presents measures to evaluate forecast accuracy. Each method has a corresponding R function. The section too demonstrates the way of using an R function to test residuals.

The author tested R code with Microsoft R Open iv.0.2 on Windows 10 Habitation ten.0 <X64>. For the sake of sit-in, the sample lawmaking uses some time serial from the "fpp2" open up source packages. Several forecasting packages are capable of performing time-series data assay. This article uses the "forecast" package, a rock-solid framework for time series forecasting (lm, 2020). The article also uses the role "sma()" in the "smoothen" package to compute moving averages.

1 – Tendency-Seasonal Analysis

The trend-seasonal analysis is i of the well-nigh important methods for analyzing time series in business. This method estimates the iv basic components of a time series: secular tendency (T), cyclical effect (C), seasonal variation (S) and residual upshot (R). Since the chief goal of fourth dimension serial analysis is to create forecasts (Siegel, 2012), the starting time footstep in time series analysis must carefully examine the plot representing the data for validation (Shumway & Stoffer, 2016).

i.1 Visualizing Time Series

Visualization helps discover the underlying behavior of a fourth dimension series and detect fourth dimension series anomalies. We usually see several singled-out patterns in a time series. Based on these patterns, we can so select appropriate analysis methods. Many tools, for instance, R, Python, and Excel are capable of visualizing time series. We often present time series data in a time series plot, which plots each observation against the time at which we measured (Moore et al., 2018).

When performing time series analysis in R, we can store a time series equally a time serial object (i.e., a ts object). For case, we employ the post-obit R commands to store the data shown in Table 1. When the time intervals are less than 1 yr, for example, "monthly," we should utilize the "frequency" argument in the office "ts". For monthly fourth dimension series, we fix frequency = 12, while for quarterly time serial, nosotros fix frequency = iv (Coghlan, 2018). The "autoplot()" command automatically produces an appropriate plot based on the outset argument. When nosotros pass a ts object to the command, the command produces a time series plot.

            library(forecast) y <- ts(c(4,eight,12,14,22,27,14,17,17,10,12,xvi,22,xv,11), start=2006) autoplot(y, xlab = "Yr", ylab = "Number of Newly Joined Members")          

Figure ane shows the yearly number of new members from 2006 to 2020. The fourth dimension serial plot indicates that MSSQLTips.com started with four authors. From 2006 to 2011, the number of newly joined members increased every yr, and the number reached the first height in 2011. The number had a sudden drop in 2012. Then, the number went up and down and reached the dip in 2015. The number in 2011 seems to be an outlier, and the other numbers fluctuate around the average.

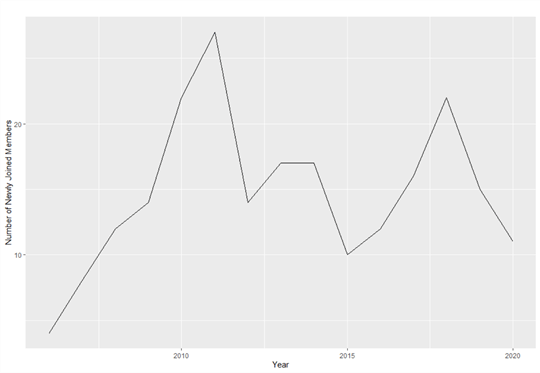
Figure 1 The yearly numbers of new team members observed from 2006 to 2020

The fourth dimension serial presented in Table 1 is nerveless on an annual basis. There was no chance to model a within-year design from the observed values recorded once a yr; therefore, the plot did not demonstrate seasonality. Seasonality is a characteristic of the time serial in which data present anticipated and somewhat regular changes that repeat every calendar twelvemonth. The "fpp2" bundle contains a monthly Australian electricity demand series (Hyndman & Athanasopoulos, 2018). We apply the post-obit R code to plot the fourth dimension series. It is worth noting that the part "window()" extracts a subset of the time series.

            library(fpp2) aelec <- window(elec, start=1980) autoplot(aelec, xlab ="Year", ylab = "GWh")          

Figure ii illustrates the monthly Australian electricity need from 1980 to 1995. In the time series plot, nosotros observe an increasing trend in demand too as a seasonal design. At the kickoff of each year, the demand was at a dip point. And so the need exhibited rises. The need might fall in April, but usually reached a peak in July. Afterward July, the need decreased. In the residuum of the yr, the demand might fluctuate, however, reached the adjacent dip signal at the end of the year. This pattern repeats every year from 1980 to 1995.

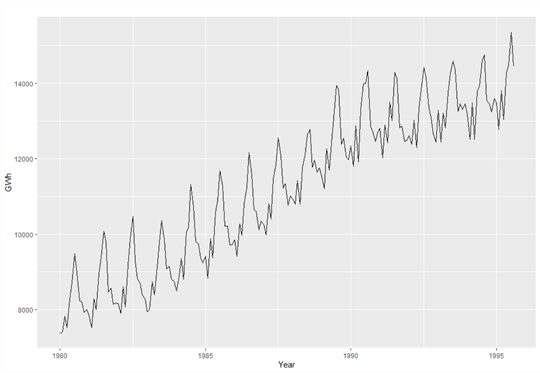
Figure 2 Monthly Australian electricity demand from 1980–1995

In Figure 2, the values fluctuate around the trend, and all the magnitude of the seasonal design falls nearly inside a band of constant width. In practice, we may find that the variability of the magnitude increases over time, as shown in Figure 3. This effigy illustrates that the magnitude changes over time. The variability spreads out as the trend increases. We executed the following R commands to produce the figure:

            library(fpp2) autoplot(a10, xlab="Yr", ylab="$ million")          

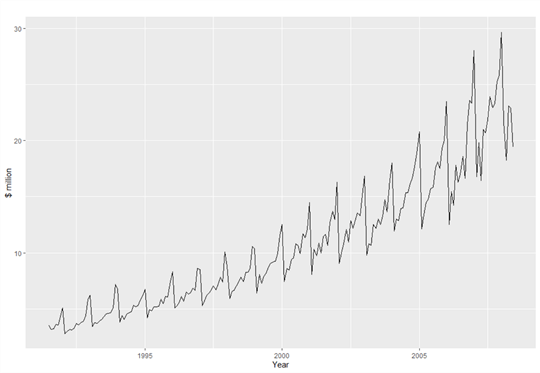
Figure 3 Monthly sales of antidiabetic drugs in Australia

1.ii Components of a Time Series

We take seen several time series plots and observed some patterns in time series. These patterns comprise one or several components combined to yield the time series information (Gerbing, 2016). We tin analyze each component separately and then combine each component's predictions to produce forecasts (Hanke & Wichern, 2014). The approach of estimating four cardinal components of a time series is called tendency-seasonal analysis. Here are the definitions of 4 components:

(1) Secular trend (T): A long-term increase or decrease in the data. The form of the trend design may exist linear or non-linear.

(2) Cyclical effect (C): The gradual up-and-down fluctuation (sometimes called business cycles) against the secular trend where the fluctuations are not of a stock-still frequency. For most business and economic information, the cycle in the cyclic component is over one year.

(three) Seasonal variation (South): the fluctuations that recur during specific portions of the year (eastward.chiliad., monthly, or quarterly). In the business and financial world, nosotros usually mensurate seasonal component in quarters.

(iv) Residual outcome (R): Balance variations that remain after the secular, cyclical, and seasonal components have been removed. The rest event is purely random.

In practice, the cyclical variation does not always follow any definite trend; therefore, cycles are often challenging to place. Many people confuse the cyclic component with the seasonal component. Nosotros can examine the frequency to distinguish them. If the frequency is unchanging and associated with some aspect of the calendar, then the design is seasonal. The cyclic component rarely has a fixed frequency.

Moreover, the magnitude of cycles appears to be more than variable than the magnitude of seasonal patterns. The boilerplate length of cycles in a time series is longer than the seasonal patterns (Hyndman & Athanasopoulos, 2018). It is not easy to deal with the cyclic component of a time series. For the sake of simplicity, we combine the tendency and cycle into a unmarried trend-bicycle component (or just call it the trend component). Then, we concentrate on merely three components, T, South, and R (Hyndman & Athanasopoulos, 2018). We visualize these components in Section 1.3.

1.3 The Condiment vs. The Multiplicative Model

The tendency (T), cyclic (C), seasonal (S), and residue (R) components combine to class the pattern underlying the time series. To proceed things relatively elementary, we combined the cyclic component into the trend component. Therefore, we consider only three components, T, S, and R. To describe the mathematical relationship between the components and the original series, we take two widely used models: additive and multiplicative. The additive model treats the fourth dimension series values as a sum of these components:

On the other side, a multiplicative model that treats the time series values as the production of these components:

The condiment model expresses the S and R components equally a fixed number of units to a higher place or below the underlying tendency at a fourth dimension point. In contrast, the multiplicative model expresses the S and R components as percentages in a higher place or below the underlying tendency at a time point. For the additive model, the variations of the Southward and R change picayune over time. The time series illustrated in Figure 2 indicates this kind of behavior. Nonetheless, Effigy 3, the multiplicative model, reveals a distinct blueprint in which the S and R components increment when the T component increases. We can write the multiplicative model in a grade of an additive model by taking natural logarithms:

The "forecast" bundle provides the function "decompose()" to decompose a seasonal time series into the trend, seasonal and residue components. We use the post-obit R code to decompose the time series shown in Figure 2. The output of the R code, shown in Figure four, illustrates the three components. Then we tin can obtain forecasts by imposing the forecasts produced from the seasonal component on the forecasts from the trend component.

            library(fpp2) library(forecast) aelec <- window(elec, start=1980) aelecComp <- decompose(aelec,type=c("additive")) autoplot(aelecComp)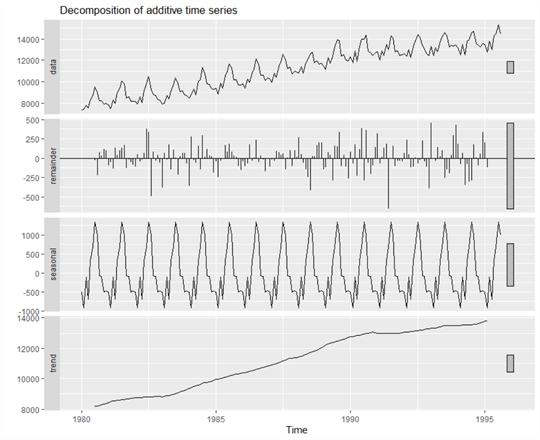          

Figure 4 The decomposition of the additive time serial

Note that the "type" statement used in the function specifies the blazon of the model. The time serial illustrated in Figure three is a multiplicative model. Nosotros use the following R code to decompose the time series. Figure 5 shows the three components, T, Due south, and R. We also can admission the estimated values of the T, S, and R components through variables "a10Comp$trend," "a10Comp$seasonal" and "a10Comp$random," respectively.

            library(fpp2) library(forecast) a10Comp <- decompose(a10,type=c("multiplicative")) autoplot(a10Comp)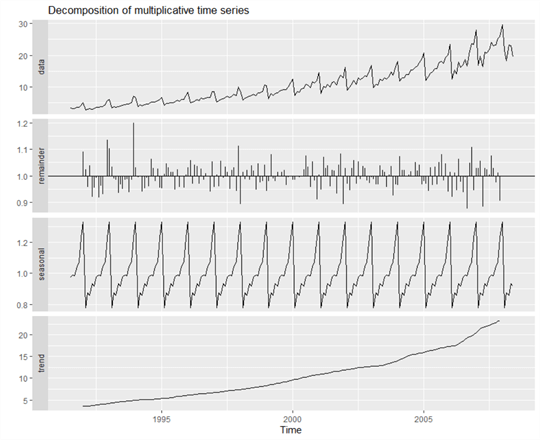          

Effigy 5 The decomposition of the multiplicative time series

2 Forecasts Based on Time Series

A forecast is a prediction of a future value of a time series (Moore et al., 2018). Most people are familiar with the weather condition forecast which meteorologists set for united states. In daily business organisation activities, nosotros perform forecasting in many situations, such every bit budgeting and inventory management. Even though we take scientific methods, forecasting is not an verbal scientific discipline, simply is as art and science. Not only should we create sophisticated mathematical models, just we should apply experience, judgment, and intuition to choose the right models. No single model works all the fourth dimension. We should continuously evaluate different models and ever select advisable ones.

2.i Exploring Characteristics of Forecasting

Knowing no other factors that may influence a fourth dimension series, we assume we can estimate future values of the serial from the by values. However, many people say that time series forecasting is ever wrong because a forecast does non precisely hit the number information technology predicts. This skepticism comes from several causes, just perhaps the most central is a misunderstanding of the forecast. We should know some characteristics about forecasting, and so we can translate forecasts correctly. Even though forecasting techniques vary widely, Stevenson summarized several forecasting characteristics in common (Stevenson, 2012):

(1) Forecasting techniques generally assume that the trend, circadian, and seasonal components are stable, and past patterns will go on.

(2) Forecast errors are unavoidable because fourth dimension series contain random errors.

(iii) A forecast usually represents an estimate of average. Forecasts for a group are more accurate than forecasts for individuals in the group.

(4) Longer-range forecasts tend to exist less authentic than short-range forecasts considering the one-time contains more uncertainties than the latter.

2.2 Uncomplicated Forecasting Methods for Time Serial

The time serial differs from cantankerous-sectional data in that the sequence of observations in a time series is critical. The historical data in the time series tin provide clues nigh the futurity. In this department, we explore these forecasting methods:

• The mean method
• The Naïve method
• The seasonal naïve method
• The uncomplicated moving average method

These forecasting techniques are piece of cake to understand and utilise. Business organisation users understand the limitations of these techniques, adjust forecasts accordingly, and apply them in the advisable circumstances. Not surprisingly, simple forecasting techniques enjoy widespread popularity, while sophisticated techniques lack trust (Stevenson, 2012). As Droke mentioned: "Nothing distills the essence of supply and demand similar the chart. And nothing distills the chart quite like the moving average" (Droke, 2001).

two.ii.1 Preparing Information

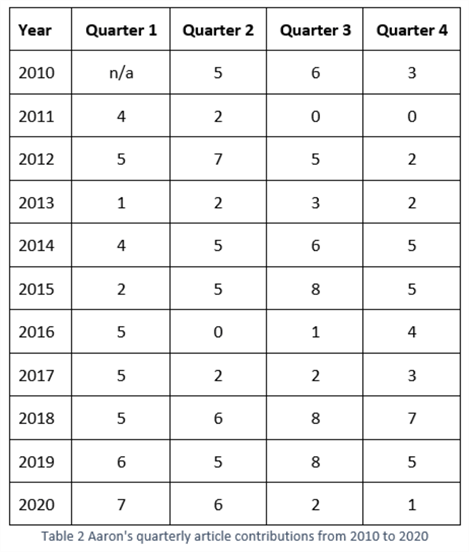
Aaron Bertrand is a passionate technologist with rich experience in SQL Server Technologies. He joined the MSSQLTips.com team in 2010. From and then on, he has been writing articles for MSSQLTips.com. As of this writing, he has contributed 177 articles. Tabular array ii shows his quarterly article contributions from 2010 to 2020.

In do, we may have different kinds of time series data. For case, in some circumstances, times series are only approximately evenly spaced. Sometimes, even though time series are evenly spaced, they miss some values. For simplicity, in this article, nosotros concentrate on analyzing evenly spaced time series that do not miss any values. Nosotros use the following R lawmaking to construct a time series object and plot the time series. Figure vi illustrates the time series plot, which does not reveal an apparent seasonality.

            Library(forecast) contributions <- c(v,6,three,iv,2,0,0,5,7,5,2,i,2,3,ii,4,5,6,5,2,5,8,v,five,0,1,iv,5,two,2,three,5,half-dozen,eight,vii,half dozen,5,viii,v,7,6,2,one) contributions.ts <- ts(contributions, frequency = 4, start = c(2010,2)) autoplot(contributions.ts,xlab = "Year", ylab = "Number of Tips")          

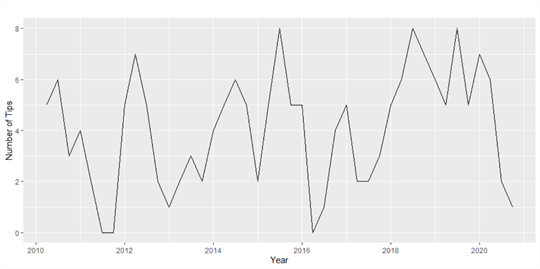
Figure 6 Aaron's quarterly article contributions from 2010 to 2020

Nosotros do not forecast noise; therefore, we should remove dissonance and detect the stable components. As nosotros mentioned in Section ane.2, nosotros concentrate on these 3 components: T, Southward, and R. In order to identify these components, we can invoke the function "decompose()" in R. The post-obit code demonstrates a way of decomposing serial, accessing these components, and plotting these components.

            contributions.comp <- decompose(contributions.ts) # Admission components contributions.comp$trend contributions.comp$seasonal contributions.comp$random autoplot(contributions.comp)          

Figure vii illustrates the three components. At any time indicate, a data value in the time series is the three components' sum. A balance (i.e., residual) above the mid-line indicates that a information value is larger than the sum of T and S components. If a remainder is below the mid-line, nosotros tin conclude that the data value is smaller than the sum of T and S components. Even though the plot illustrates an Due south component, the S component'due south magnitude is much smaller than the T component. Therefore, we say that the seasonality is weak. Although the T component moves up and downward equally time goes on, information technology exhibits a slightly upward trend.

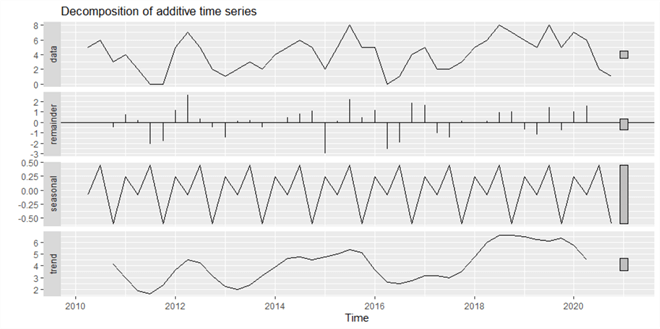
Figure 7 The time series decomposition into T, S and R components.

2.ii.two The Hateful Method

Assuming every slice of data in a time serial is equally useful to predict all future values, nosotros use the boilerplate of the time series to represent the forecasts. This method works best when a time series does non contain significant T and S components, such every bit the time series shown in Figure seven. The forecasts using this method are stable, but they may not recognize all the patterns. We can utilise the following formula to implement this method (Hyndman & Athanasopoulos, 2018):

where denotes the estimate of based on the values , and is the forecast horizon.

Averaging numeric values is a simple calculation. We can compute the mean by hand or using tools such equally Excel. Substituting into the formula with values in Table ii, we find the mean value, i.e., 4.069767. The number of contributions is always an integer. Nosotros recommend that the numeric format of a forecast be the same style as the historical data. Therefore, using the mean method, loosely speaking, nosotros predict Aaron volition write iv articles every quarter in 2021.

The mean method presents us with a single number (i.e., point forecast). A point forecast, ordinarily the mean of the probability distribution, represents an estimate of the boilerplate number of contributions if the period, such as the showtime quarter in 2021, repeats many times over. However, nosotros can but run into one case of the get-go quarter in 2021; therefore, nosotros never know the real average. To make the forecasting more meaningful, we should know other statistical information well-nigh the forecasts, such as prediction intervals.

A prediction interval is an interval for the prediction of private observation. A 95% prediction interval indicates that, if a future result repeats, that take a chance of a specific characteristic measured from the event fall within the prediction interval is 95%. The office "meanf ()" in the "forecast" packet tin can render forecasts and prediction intervals. The following R statements produce the forecasting model, plot the forecasts, and impress the model summary.

            library(forecast) contributions <- c(5,vi,3,iv,2,0,0,5,vii,five,2,1,two,3,two,four,v,half-dozen,v,two,v,8,5,5,0,1,iv,5,two,two,3,5,half-dozen,8,7,6,5,8,v,7,6,2,i) contributions.ts <- ts(contributions, frequency = 4, start = c(2010,ii))   # Use meanf() to forecast quarterly contributions in 2021 contributions.fc <- meanf(contributions.ts, h=iv)   # Plot and summarize the forecasts autoplot(contributions.fc,xlab = "Year", ylab = "Contributions") summary(contributions.fc)          

Effigy 8 illustrates the forecasts of the number of articles Aaron volition write in 2021. The short horizontal blue line on the right represents the point forecasts for the year 2021. From the plot, we can as well notice lxxx% and 95% prediction intervals. The 95% prediction interval contains the true value of the future values with a probability of 95%, while the take a chance of the 80% prediction intervals contains the true number is 80%. The 95% prediction interval is wider than the 80% prediction interval.

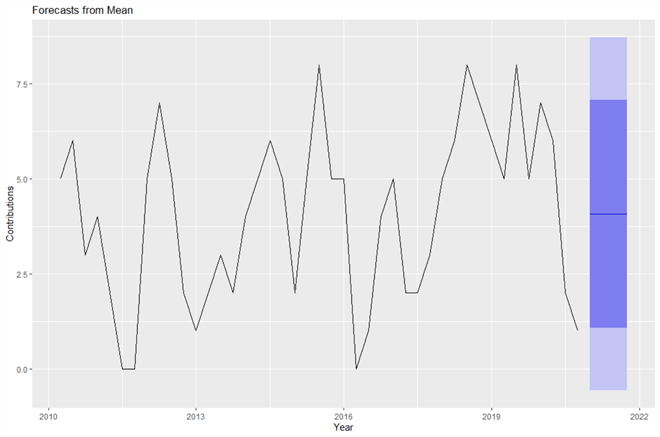
Figure 8 Predict number of Aaron'southward contributions using the mean method

The "summary()" function produces the model data, mistake measures, bespeak forecasts, an 80% prediction interval for the forecasts, and a 95% prediction interval, shown as follows. Nosotros observe some impossible values in the intervals since the number of manufactures should be not-negative. These prediction intervals do not seem trustworthy. For the sake of simplicity, nosotros tin can adjust the intervals past removing all impossible values.

The output shows that, loosely speaking, Aaron will write iv manufactures every quarter in 2021, with a 95% prediction interval of [0, 9]. Even though we practise non know the true value, we are 95% confident that the true value is between 0 and 9. The hateful method does not utilise the ordering information in the time series; therefore, all point forecasts take the aforementioned value and all intervals have the same width.

            Forecast method: Mean Model Information: $mu [1] iv.069767 $mu.se [1] 0.3464667 $sd [1] 2.271934 $bootstrap [1] Fake $telephone call meanf(y = contributions.ts, h = 4) attr(,"course") [one] "meanf" Fault measures:                         ME     RMSE      MAE  MPE MAPE     MASE      ACF1 Training set -1.239117e-16 2.245361 1.925365 -Inf  Inf 0.736169 0.5011576 Forecasts:         Point Forecast   Lo 80    Hello fourscore      Lo 95    Howdy 95 2021 Q1       four.069767 1.07743 7.062105 -0.5681876 8.707722 2021 Q2       4.069767 i.07743 7.062105 -0.5681876 8.707722 2021 Q3       four.069767 1.07743 seven.062105 -0.5681876 8.707722 2021 Q4       iv.069767 1.07743 seven.062105 -0.5681876 8.707722 >          

2.2.3 The Naïve Method

The naïve method, one of the simplest forecasting methods, does not consider the furnishings of T and S components. When using this method, the forecast for a given period is the value of the previous menstruation. The naïve method seems to piece of work better with data reported on a daily or weekly basis or in situations that show no T or S components (Black, 2013). This method provides a useful criterion for other forecasting methods.

Nosotros use the post-obit equation to represent the naïve method mathematically (Hyndman & Athanasopoulos, 2018):

where denotes the approximate of based on the data , and is the forecast horizon.

According to the equation, given h = 4, nosotros predict Aaron will contribute one article in every quarter of 2021. This obvious adding only gives bespeak forecasts. To find the prediction intervals, we utilise the function "naïve()" in the "forecast" package. We use the following R script to visualize the forecasts, and impress prediction intervals.

            library(forecast) contributions <- c(v,half-dozen,3,four,ii,0,0,5,7,five,ii,1,2,three,two,4,5,6,five,2,5,8,5,5,0,ane,4,five,2,2,3,5,6,eight,vii,6,5,8,5,7,6,ii,one) contributions.ts <- ts(contributions, frequency = 4, get-go = c(2010,2))   # Use naive() to forecast contributions in 2021 contributions.fc <- naive(contributions.ts, h=four)   # Plot and summarize the forecasts autoplot(contributions.fc) summary(contributions.fc)          

Figure 9 illustrates the forecasts of the number of articles Aaron will write in 2021. The blue line on the right is the betoken forecasts for the yr 2021. The 80% prediction interval is in the night shaded region, and the 95% prediction interval is in the light shaded regions. We observe that the longer-ranger forecasts accept wider prediction intervals. When the prediction interval is wider, the forecasts have more than uncertainties, and the predicted values may become less meaningful.

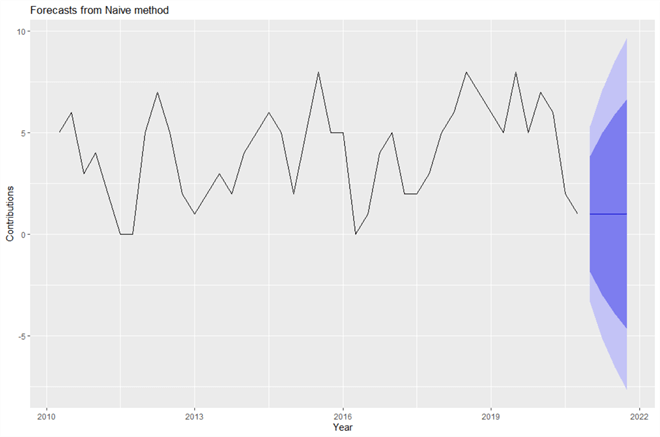
Figure 9 Predict number of contributions using the naive method

The output of the "summary()" function, shown as follows, contains the model information, error measures, indicate forecasts, 80% prediction intervals for the forecasts, and 95% prediction intervals. By removing all impossible values in the intervals, Aaron's forecasted number of articles in the first quarter of 2021 is almost one, with a 95% prediction interval [0, five]. That is to say, we are 95% confident that the true number is between 0 and 5.

            Forecast method: Naive method Model Data: Call: naive(y = contributions.ts, h = 4)  Residuum sd: 2.2394  Error measures:                      ME    RMSE      MAE  MPE MAPE     MASE        ACF1 Grooming set up -0.0952381 2.21467 i.857143 -Inf  Inf 0.710084 -0.02135027 Forecasts:         Indicate Forecast     Lo 80    Hullo lxxx     Lo 95    Hi 95 2021 Q1              1 -1.838213 three.838213 -iii.340673 5.340673 2021 Q2              i -3.013840 5.013840 -v.138638 seven.138638 2021 Q3              ane -iii.915930 5.915930 -6.518266 8.518266 2021 Q4              1 -4.676427 6.676427 -7.681346 nine.681346 >          

2.2.four The Seasonal Naïve method

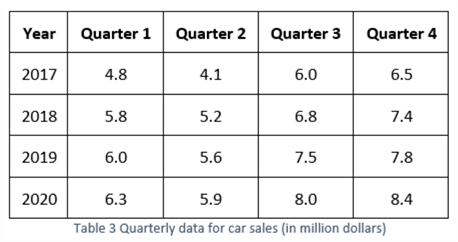
We tin can brand several adaptations to the naïve method. When nosotros have highly seasonal data, the forecast for the current season is the bodily value of the concluding season. For instance, if the time series for Aaron's contributions were seasonal, the forecast for the first quarter of 2021 should be the number of articles he wrote in the first quarter of 2020, i.east., seven. This variation of the naïve method is called the seasonal naïve method. Nosotros utilise information from University's tutorial (Academy, 2013) to show the mode of using the seasonal naïve method. We present the data in Table 3.

The time series plot shown in Figure 10 demonstrates the high seasonality and an upwardly trend as well. Other forecasting methods, for example, the method presented in Academy's lecture (Academy, 2013), may do better than the seasonal naïve method. However, complex methods do non guarantee accuracy. If we tin utilise a more straightforward method and get the same accuracy level, nosotros adopt the simpler 1.

When we have quarterly data, the starting time quarter's forecast in a twelvemonth is equal to the quarter'south observed value in the previous year. Applying the same rule to other quarters, nosotros have forecasts for other quarters. The car sales in quarters 1, 2, 3, and 4 of the yr 2020 are 6.3, 5.9, 8.0, and 8.4, respectively. Therefore, the forecasts for quarters 1, 2, 3, and iv in 2021 are half dozen.3, five.ix, 8.0, and viii.4, respectively. Hyndman and Athanasopoulos concluded a mathematical expression to stand for this method:

where thou is the seasonal catamenia, and k is the integer role of (h−one)/m.

The "forecast" bundle provides a function "snaïve()" to make a forecast model. We use the following R statements to produce the forecasting model, plot the forecasts, and impress out a summary of the model.

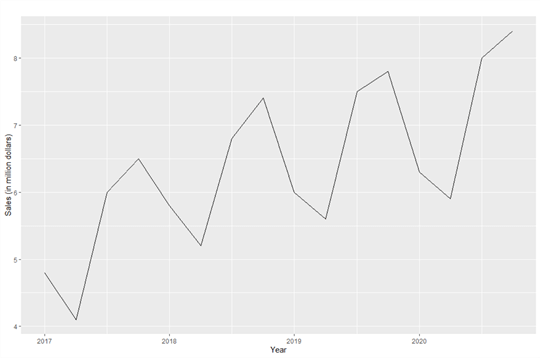
            library(forecast) sales <- c(four.8,iv.1,6.0,6.5,5.8,5.two,6.8,7.4,6.0,five.6,7.5,vii.8,6.3,five.nine,8.0,eight.iv) sales.ts <- ts(sales,frequency=iv, start=c(2017,1)) autoplot(sales.ts,xlab = "Year", ylab = "Sales (in million dollars)")   # Use snaive() to forecast sales in 2021 sales.fc <- snaive(sales.ts, h=4)   # Plot and summarize the forecasts autoplot(sales.fc) summary(sales.fc)          

Figure eleven shows the forecasts for car sales in the four quarters of 2021. The bluish line represents the point forecasts, and the shaded regions illustrate predictions regions. We find that the fourscore% prediction intervals lies within of the 95% prediction intervals. The seasonal naïve method uses the value from the beginning quarter of 2020 to predict the first quarter of 2021. The prediction of the 2d quarter of 2021 uses the second quarter of 2020, and and so on. Nevertheless, this method does not recognize the upwardly trend in the fourth dimension series.

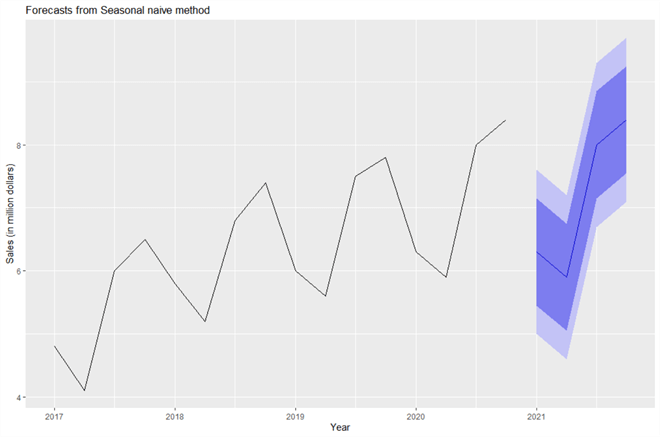
Figure xi Predict automobile sales using the seasonal naïve method

The output of the "summary()" function, shown as follows, contains the model information, error measures, signal forecasts, 80% prediction intervals for the forecasts, and 95% prediction intervals. In the first quarter of 2021, the point forecast is 6.3 one thousand thousand dollars, and the 95% prediction interval is [5.0, 7.6]. The prediction intervals limited the doubt in the forecasts.

            Forecast method: Seasonal naive method Model Data: Call: snaive(y = sales.ts, h = 4)  Balance sd: 0.2985  Error measures:               ME      RMSE MAE      MPE     MAPE MASE      ACF1 Preparation ready 0.half dozen 0.6645801 0.6 9.208278 9.208278    ane 0.4693878 Forecasts:         Signal Forecast    Lo lxxx    Hello lxxx    Lo 95    Hi 95 2021 Q1            half dozen.3 v.448306 vii.151694 4.997447 7.602553 2021 Q2            five.9 5.048306 6.751694 4.597447 seven.202553 2021 Q3            8.0 7.148306 8.851694 6.697447 nine.302553 2021 Q4            viii.4 seven.548306 ix.251694 7.097447 9.702553 >          

2.2.5 The Unproblematic Moving Average Method

The simple moving boilerplate method is, past far, the most widely used (Pring, 2014). Nosotros compute an average by adding up a set of data and dividing the sum by the number of items in the set. To "move" the average, we remove the outset item in the set, append a new item, and then average the set. When nosotros computer moving averages for a fourth dimension series, the averages form a new time series. The new time series becomes flat because the calculation process removes the rapid fluctuations. The moving average method works best when the time series is trending.

There are ii major ways of using moving averages: one-sided moving averages and 2-sided moving averages (Hyndman, 2010). Nosotros explore the one-sided moving averages in this article. Given a time point, nosotros boilerplate a subset that comprises its almost contempo actual data values. The average is the forecast of the time point. When the fourth dimension point moves forward, we get ane-sided moving averages (or trailing moving averages). The clarification of the method looks more complicated than it is. If nosotros use Due north to announce the length of the subset, we tin can use this equation to compute the moving averages:

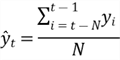
For sake of the simplicity, the calculation for N = 4 should look like the post-obit equation:

Tabular array 4 contains true values in 43 periods. We apply this method to these values. For the sake of demonstration, we select N = iv, which means we can only beginning the calculation later nosotros have collected four periods' data. Nosotros calculate the outset moving boilerplate forecast (i.due east.,4.fifty) for menses 5. When the true value (i.e.,2) in period v is available, nosotros utilise the truthful value to compute the forecast for catamenia half-dozen, i.e., iii.75. Nosotros repeat the procedure until we find the forecast (i.e.,four.00) at period 44. Therefore, the forecast for the number in the commencement quarter of 2021 is four.

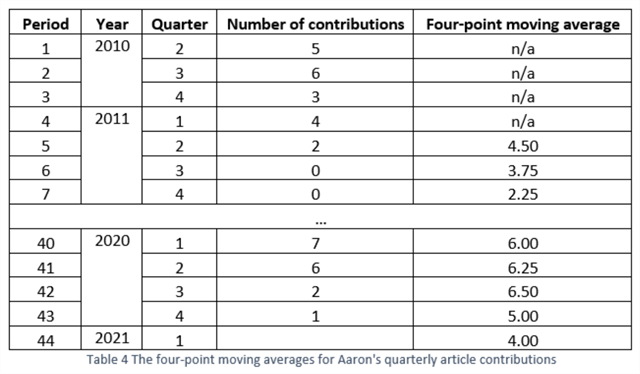
This practice selected four information points; therefore, these averages are chosen four-point moving averages. When the number of data points, i.e., the subset's length, is small, the forecast is volatile. When the length is considerable, the forecast is stable. As a rule of pollex, we typically select 1, ii, iii, four, or 5 data points for a non-seasonal fourth dimension serial. We use the length of an annual bicycle as the subset's length when analyzing seasonal time series, for instance, selecting iv information points for quarterly data and selecting 12 information points for monthly data (William & Sincich, 2012). Forecast accuracy metrics assist select the number of data points. We option one metric we trust and observe out which N can bring u.s. better accuracy.

The "smooth" packet in R provides the function "sma" to compute the elementary moving average (Svetunkov, 2021). We use the following R statements to produce the model, print out a summary of the model, and print the forecasts and prediction intervals.

            library(smooth) contributions <- c(five,6,iii,4,2,0,0,five,7,5,ii,i,2,three,2,4,5,6,5,ii,five,8,5,5,0,1,4,5,2,2,3,v,vi,viii,7,6,5,eight,5,7,half dozen,two,ane) contributions.ts <- ts(contributions, frequency = iv, first = c(2010,2))   # Use sma() to forecast number of Aaron's contributions in 2021 contributions.fc <- sma(contributions.ts, social club=4, h=4,silent=Faux) # Impress model summary summary(contributions.fc) # Print the forecasts fc <- forecast(contributions.fc) print(fc)          

Figure 12 presents the forecasts of the number of articles Aaron volition write in 2021. The solid blue line represents the point forecasts for the four quarters in 2021. The plot of the moving averages (i.e., the fitted values) is smoother than the original series. When we increase the value of North, the plot of the moving average becomes flatter. The plot does non illustrate prediction intervals, but we can observe the lower leap and upper leap from fc$lower and fc$upper, respectively.

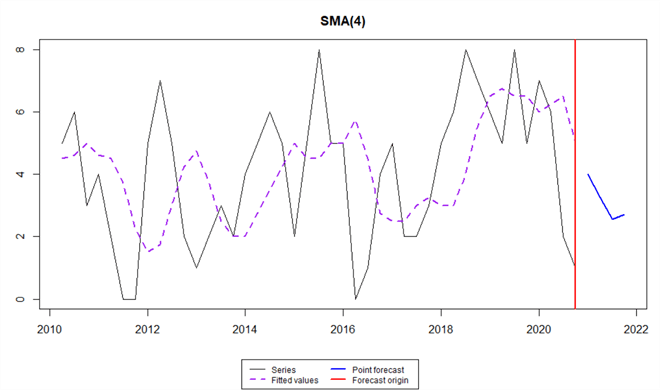
Effigy 12 Predicting number of contributions using the elementary moving average method

The output of the role "summary()", shown equally follows, contains the model data, and accuracy measures. The office "forecast()" gives signal forecasts and 95% prediction intervals. By removing all impossible values, Aaron'due south forecasted number of manufactures in the starting time quarter of 2021 is about four, with a 95% prediction interval [0, 9].

            > # Impress model summary > summary(contributions.fc) Fourth dimension elapsed: 0.07 seconds Model estimated: SMA(4) Initial values were produced using backcasting.   Loss office type: MSE; Loss office value: vi.194 Fault standard deviation: 2.5488 Sample size: 43 Number of estimated parameters: 2 Number of degrees of freedom: 41 Information criteria:      AIC     AICc      BIC     BICc  204.4430 204.7430 207.9654 208.5296  > # Impress the forecasts > fc <- forecast(contributions.fc) > print(fc)         Bespeak forecast Lower jump (2.v%) Upper jump (97.5%) 2021 Q1       4.000000          -1.147330            ix.147330 2021 Q2       iii.250000          -2.055746            8.555746 2021 Q3       2.562500          -2.981717            8.106717 2021 Q4       2.703125          -3.194431            8.600681 2022 Q1       3.128906          -iii.281871            nine.539683 2022 Q2       2.911133          -3.762586            9.584852 2022 Q3       2.826416          -four.139641            9.792473 2022 Q4       ii.892395          -four.381565           ten.166355 2023 Q1       2.939713          -4.635420           10.514845 2023 Q2       2.892414          -four.946159           10.730987 >          

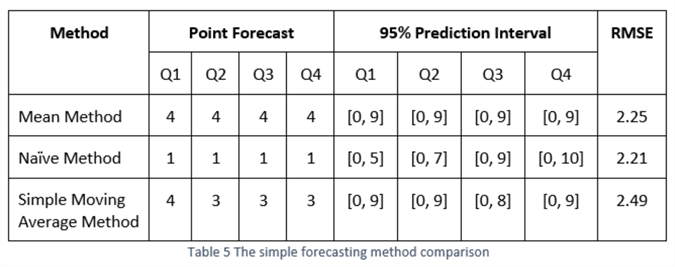
We accept implemented three methods to forecast how many articles Aaron volition write for MSSQLtips.com in each quarter of 2021. Tabular array 5 shows the forecasts produced past the iii unproblematic forecasting methods. The RMSE column shows the root-mean-square errors, one of the nigh meaningful accurateness measures. We introduce the accuracy measures in the next section. Since the 95% prediction intervals are too wide according to the writer's intuition, the forecasts may be accurate but not meaningful. This scenario frequently happens in practice, and we should look at other techniques. We concentrated on the four elementary forecasting methods in this article.

2.3 Assessing Forecast Accuracy

We used three methods to forecast the numbers of Aaron's contributions in 2021. To determine which method made a good forecast, we measure forecast accuracies. We can calculate forecast accuracy by analyzing the forecast errors, which are the differences between the bodily future values and the respective predicted values. The iii widely accepted measures are the mean absolute divergence (MAD), the mean absolute percentage error (MAPE), and the root mean squared mistake (RMSE). Most software packages tin can automatically calculate the values of these measures.

2.iii.1 The Mean Absolute Deviation (MAD)

The mean absolute deviation (MAD) measures forecast accuracy by averaging the accented values of the forecast errors. Considering MAD is like shooting fish in a barrel to understand and calculate, we can use this measure to compare forecasting methods applied to a unmarried time series (Hyndman & Athanasopoulos, 2018). The MAD is in the same units every bit the original series; therefore, it is not meaningful to compare this measure betwixt forecasts with different units. We can compute the MAD by the following equation:

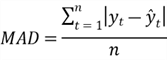
Let us compute the MAD of the model produced in Section two.2.two:

MAD has another name, i.e., MAE (the Hateful Absolute Fault). The "meanf()" function used in Section two.2.2 obtained a value of i.925365 for the MAE. The result from the R office agrees with the manual calculation.

2.3.ii The Mean Absolute Pct Error (MAPE)

Different fourth dimension series may have different units, for example, million dollars and gallon. When comparing forecasting methods practical to multiple fourth dimension serial with unlike units, we tin use the mean absolute per centum fault (MAPE) that does non associate a unit. Sometimes, when the magnitude of observed values is meaning, information technology is easy to interpret the forecast errors in terms of per centum.

To calculate the MAPE, we first notice the absolute mistake at each time point divided by the observed value at this point. We then average these quotients and write the average in percentage. The following expression represents this adding procedure:

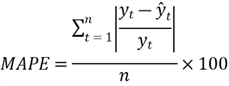
Let us calculate the MAPE to evaluate the model produced by the mean method in Section 2.ii.2:

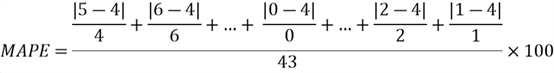
Because of the value of 0 in the time series, nosotros cannot compute the MAPE for the forecasts, while the "meanf()" function return "Inf" for this case. The MAPE has other limitations. For example, if a time series contains very pocket-sized values, the MAPE tin be very large. Kolassa summarized the limitations of the MAPE when he answered a question on the spider web (Kolassa, 2017).

2.iii.three The Root Hateful Squared Error (RMSE)

The root hateful squared fault (RMSE), one of the almost meaningful measures, is the square root of the average of squared errors. We do not want large errors in the forecast; therefore, we want the measure out to be sensitive to big errors. When nosotros square the mistake, a large error results in a larger value, and a small error produces a smaller value. Hither is the formula to compute the RMSE:

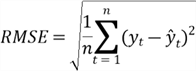
Permit us compute the RMSE to evaluate the model in Section two.2.ii. The value of RMSE computed past the function "meanf()" is 2.245361, which is shut to the manual calculation from the post-obit equation.

The RMSE measures the variance in forecast errors, while the MAD estimates the standard difference of the forecast error and allows users to approximate the expected value. The MAPE measures the degree of error in predicting compared with the true value. Each measure tells united states of america a different story nearly the forecast accuracy. When comparing forecasting methods, a expert rule is to cull the method with the smallest RMSE.

ii.3.iv Examining the Residuals

We covered iv methods to compute betoken forecasts. However, every bit Hyndman mentioned, point forecasts tin be of almost no value without the accompanying prediction intervals (Hyndman & Athanasopoulos, 2018). Furthermore, when the prediction intervals are wide, for instance, the intervals produced in two.ii.two, the forecasts may besides not be meaningful. To compute a prediction interval at a time indicate, we consider the forecast at the time point to exist a probability distribution. The bespeak forecast is the mean of the distribution. We brand the following 4 standard assumptions [Jost, 2017] for computing predictions intervals:

1. Independence: the residuals associated with whatever two dissimilar observations are independent, i.east., the residuals are uncorrelated.
2. Unbiasedness: the hateful value of the residuals is zero in whatever sparse vertical rectangle in the residual plot. The forecasts are biased if the hateful value differs from zero.
3. Homoscedasticity: the standard divergence of the errors is the same in any thin rectangle in the residue plot.
4. Normality: at any observation, the error component has a normal distribution.

The first two assumptions make up one's mind whether a forecasting method uses all data in data to make a prediction. If the residuals do non satisfy the first two assumptions, we can improve the forecasting method. The forecasts might nevertheless provide useful information fifty-fifty with residuals that fail the white racket (i.e., a purely random time serial) test. The last two assumptions are not restrictive. Moderate departures from these assumptions take less upshot on the statistical tests and the conviction interval constructions.

The "forecast" packet provides the role "checkresiduals()" to test these assumptions. The function gives the results of a Ljung-Box test, in which a small p-value indicates the data are probably non white noise. Moreover, the function produces a fourth dimension serial plot of the residuals, the corresponding ACF, and a histogram. We invoke this office through the post-obit R script to test the residuals produced from the hateful method:

            library(forecast) contributions <- c(5,6,3,iv,two,0,0,v,7,five,2,1,2,iii,2,4,five,vi,5,2,5,eight,5,5,0,1,four,5,2,2,3,five,6,8,7,6,5,viii,5,7,half dozen,2,1) contributions.ts <- ts(contributions, frequency = four, start = c(2010,2))   # Utilise meanf() to forecast contributions in 2021 contributions.fc <- meanf(contributions.ts, h=4)   # Examining the Residuals checkresiduals(contributions.fc)          

The function prints the result of the Ljung-Box test every bit follows. The p-value is 0.03228. If we select a significance level of 0.05, we take statistical prove to reject the nil hypothesis that the residuals are independently distributed. When the residuals are not white dissonance, at that place is much room for comeback to the forecasting method.

            > checkresiduals(contributions.fc)           Ljung-Box test   data:  Residuals from Mean Q* = fifteen.305, df = 7, p-value = 0.03228   Model df: 1.   Total lags used: 8   >          

Figure 13 presents the time serial plot, the corresponding ACF, and the histogram. The time series plot reveals that the residuals are not random. If one value in the series is greater than the hateful, the adjacent value is likely greater than the mean. The ACF plot shows the first spike is outside the blue lines, which means some information in the residuals is useful in forecasting. The histogram has two peaks; therefore, the residuals have a bimodal distribution. According to Professor Hyndman, if residuals do not meet these four assumptions, we tin still use the point forecasts. However, we should not take the prediction intervals also seriously (Hyndman, datacamp).

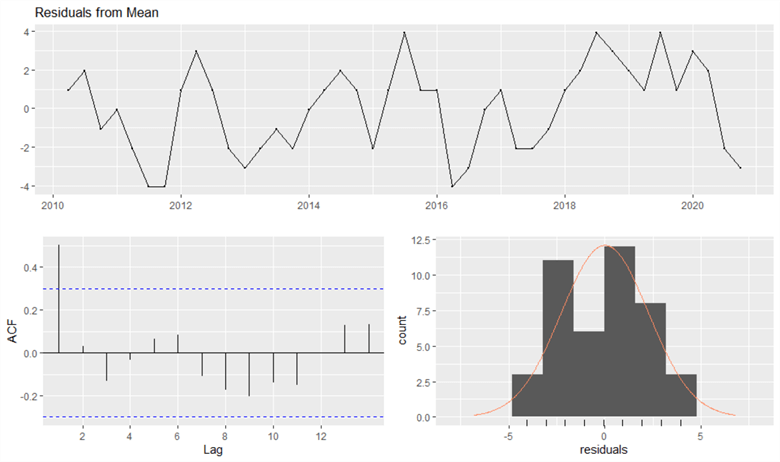
Figure 13 Remainder plots produced by the "checkresiduals()" function

Summary

The article but scratched the surface of forecasting techniques, but we hope nosotros accept opened some doors for performing time serial analysis. Nosotros covered iv elementary forecasting methods: the hateful method, the naïve method, the seasonal naïve method, and the unproblematic moving average method. Side by side, we implemented these methods to forecast time-series data. To compare these methods, we defined some accuracy measures. Afterwards examining residuum assumptions, nosotros know how to use the forecasts in business activities. Nosotros also explored some characteristics of forecasting. Knowing these characteristics helps sweep away skepticism about forecasting.

To practice these methods, we showed a mode of using R functions to explore time series data and implement forecasting methods. First, we presented R code for visualizing time serial data. We and then introduced a role to decompose a time serial into 3 components: trend, seasonal, and remainder. Next, nosotros used iv R functions to implement the four forecasting methods, respectively, and checked forecast accuracy in the function outputs. Finally, we introduced a function to test the residual assumptions.

Reference

Academy, J. (2013). Excel – Time Series Forecasting – Office 1 of 3. https://youtu.exist/gHdYEZA50KE.

Black, Grand. (2013). Business organisation Statistics: For Contemporary Conclusion Making (8th Edition). Wiley.

Coghlan, A., (2018). A Piffling Volume of R For Fourth dimension Serial. https://a-little-book-of-r-for-time-serial.readthedocs.io/.

Droke, C. (2001). Moving Averages Simplified. Marketplace Books.

Gerbing, D., (2016). Time Series Components. http://web.pdx.edu/~gerbing/515/Resources/ts.pdf.

Goodwin, P., (2018). How to Respond to a Forecasting Sceptic, Foresight: The International Journal of Applied Forecasting, International Institute of Forecasters, result 48, pages 13-16, Wintertime.

Hanke, East. J., & Wichern, D. (2014). Business Forecasting (9th Edition). Pearson.

Hyndman, R. J. (datacamp). Fitted values and residuals. https://campus.datacamp.com/courses/forecasting-in-r/criterion-methods-and-forecast-accuracy?ex=3.

Hyndman, R. J., (2010) Moving Averages. Contribution to the International Encyclopedia of Statistical Science, ed. Miodrag Lovric, Springer. pp.866-869.

Hyndman, R.J., & Athanasopoulos, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. https://otexts.com/fpp2/.

Jost, South. (2017). CSC 423: Data Analysis and Regression. http://facweb.cs.depaul.edu/sjost/csc423/.

Kolassa, South. (2017). What are the shortcomings of the Mean Accented Percentage Fault (MAPE)? https://stats.stackexchange.com/questions/299712/what-are-the-shortcomings-of-the-hateful-accented-percentage-mistake-mape.

Lm, J. (2020). Moving to Tidy Forecasting in R: How to Visualize Time Series Data. https://medium.com/@JoonSF/moving-to-tidy-forecasting-in-r-how-to-visualize-fourth dimension-series-data-1d0e42aef11a/.

Moore, S. D., McCabe, Y. G., Alwan, C. L., Craig, A. B. & Duckworth, M. W. (2010). The Practice of Statistics for Business concern and Economics (3rd Edition). W. H. Freeman.

MSSQLTips (2021). MSSQLTips Authors. https://world wide web.mssqltips.com/sql-server-mssqltips-authors/

Pring, J. M. (2014). Technical Analysis Explained: The Successful Investor's Guide to Spotting Investment Trends and Turning Points (5th Edition). McGraw-Hill Education.

Siegel, F. A. (2012). Applied Business Statistics (6th Edith). Academic Printing

Shumway, H. R., & Stoffer, S. D. (2016). Time Series Assay and Its Applications With R Examples (4th Edition). Springer

Stevenson, J. Due west. (2012). Operations Direction (11th Edition). McGraw-Loma.

Svetunkov, I. (2021). sma() - Unproblematic Moving Average. https://cran.r-projection.org/web/packages/smooth/vignettes/sma.html.

William, Yard., & Sincich, T. (2012). A 2d Course in Statistics: Regression Analysis (seventh Edition). Prentice Hall.

Next Steps

• The author presented 4 unproblematic forecasting methods in this article. Considering they are simple and piece of cake to empathise, people similar using them in practice. To learn these methods, we demand to exercise them with lots of unlike time series. After gaining much experience, we can build an intuition to determine which method is improve for a particular circumstance. Even so, in some situations, these methods do not piece of work very well. Nosotros then should brand some improvements or select other techniques. This article concentrated on the trend-seasonal assay. Another method for analyzing time serial is to use the Box–Jenkins ARIMA processes. For further studying, the author recommends Professor Hyndman's book that is bachelor at https://otexts.com/fpp3/. Rick Dobson too published several articles nearly time series and forecasting on MSSQLTips.com.
• Check out these data science related tips:
  • Basic Concepts of Probability Explained with Examples in SQL Server and R
  • Discovering Insights in SQL Server Data with Statistical Hypothesis Testing
  • Selecting a Uncomplicated Random Sample from a SQL Server Database
  • Statistical Parameter Interpretation Examples in SQL Server and R
  • Using Simple Linear Regression to Make Predictions
  • How to Compute Unproblematic Moving Averages with Time Series Data in SQL Server
  • Mining Fourth dimension Series Information by Calculating Moving Averages with T-SQL Code in SQL Server
  • Time Series Data Fact and Dimension Tables for SQL Server
  • Collecting Time Serial Data for Stock Marketplace with SQL Server
  • Exponential Moving Average Adding in SQL Server
  • Weighted vs Elementary Moving Boilerplate with SQL Server T-SQL Code
  • Mining Fourth dimension Series with Exponential Moving Averages in SQL Server
  • Introduction to SQL Server Auto Learning Services with Python

Related Articles

Popular Articles

About the author

Nai Biao Zhou is a Senior Software Programmer with xx+ years of feel in software evolution, specializing in Information Warehousing, Business organisation Intelligence, Data Mining and solution architecture design.

View all my tips

Article Last Updated: 2021-03-eleven

greerupind1987.blogspot.com

Source: https://www.mssqltips.com/sqlservertip/6778/time-series-forecasting-methods-with-r-examples/

Share this post